7 Crystal systems:
(Drag And Scroll to Animate Model)
Note 1:There are 7 crystal systems ,defined on the basis of axis of symmetry.
Note 2: It was shown by A. Bravais in 1848 that all possible three dimensional space lattice are of fourteen distinct types.
These fourteen lattice types are derived from seven crystal systems.
1. Cubic System :
Characteristic: a=b=c and α = β = γ = 90° . Cubic System is also known as the isometric system. Here all three axes are of equal length and are mutually perpendicular to each other.Here the angles are also equal and 90 degree. Some typical examples are NaCl, Zinc blende, Cu ,Diamond, Silver and Cesium chloride

Open in Full Screen
2. Orthorhombic system:
Characteristic: a≠b≠c and α = β = γ = 90° . It is also called rhombic system. It consists of three mutually perpendicular axes of unequal lengths. Few examples are di mercury dichloride, ammonium sulphate and Iodine.

Open in Full Screen
3. Tetragonal system:
Characteristic:a=b≠ c and α = β = γ = 90° . In tetragonal symmetry, the cube is elongated in one direction. The axes are still at right angle to each other, but one axis is longer ( or shorter) than the other two axes. Few examples are rutile TiO2 and lead tungstate.
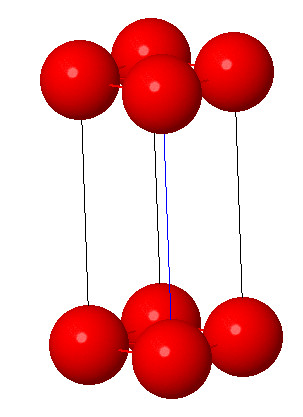
Open in Full Screen
4. Monoclinic system:
Characteristic: a≠b≠c and α = γ =90°β ≠ 120° . In monoclinic system the three axes are of unequal length and are no longer perpendicular to each other. Monoclinic system differs from rhombic symmetry in that one of axes does not make 90° with the plane of other two axes. Examples include potassium chloride and high temperature form of sulphur.
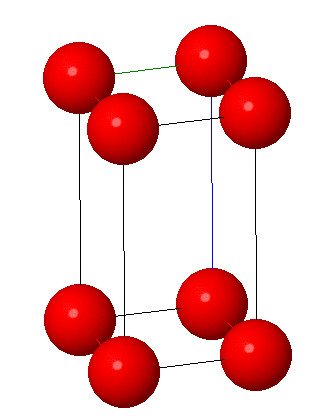
Open in Full Screen
5. Rhombohedral system:
Characteristic: a=b=c and α = β = γ ≠ 90° . It consists of three equal axes which are inclined to each other at same angle but it is not 90°. Some common examples are arsenic, antimony, bismuth and calcite.

Open in Full Screen
6. Triclinic system:
Characteristic: a ≠ b ≠ c and α ≠ β ≠ γ ≠ 90° . It consists of three unequal axes and none is perpendicular to any of the others. This system has the lowest symmetry. There is no simple axis or plane of symmetry. Example: Boric acid
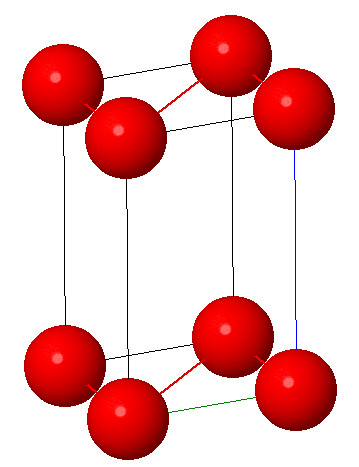
Open in Full Screen
7.Hexagonal system:
Characteristic: a=b≠c and α = β = 90°γ = 120° In this type of symmetry the atoms are arranged in the form of hexagons and these unit cell has two edges of one above length (a=b). The symmetry axis (c) is at 90° to these two axes which make an angle of 120° with one another. Graphite is a common example of hexagonal symmetry.
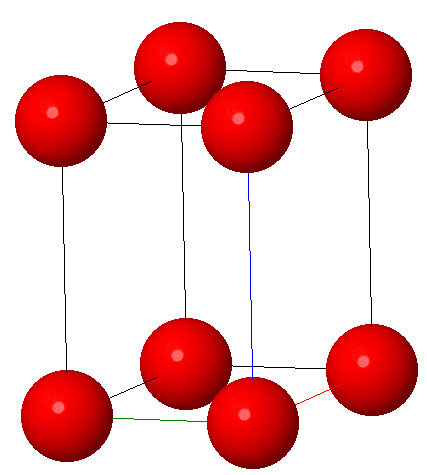
Open in Full Screen











